eyesvilla.blogg.se - Kernel density estimation

#KERNEL DENSITY ESTIMATION PDF#
#KERNEL DENSITY ESTIMATION CODE#

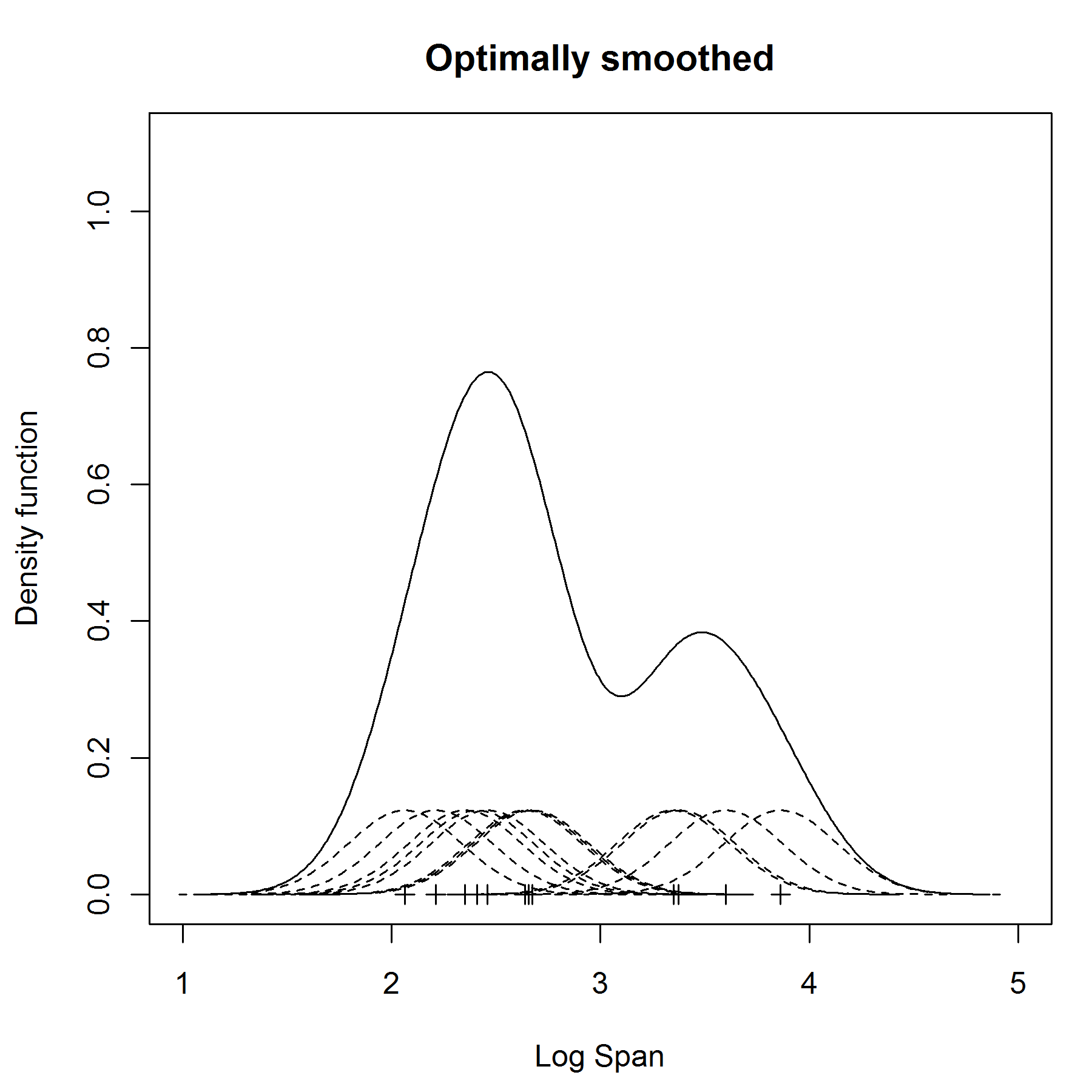
The efficiency column in the figure displays the efficiency of each of the kernel choices as a percentage of the efficiency of the Epanechnikov kernel. The Epanechnikov kernel is the most efficient in some sense that we won’t go into here. Note that seven of the kernels restrict the domain to values | u| ≤ 1. Some commonly used kernels are listed in Figure 1. Where s* = min( s, IQR/1.34) and IQR is the interquartile range of the sample data. Where s is the standard deviation of the sample. If f( x) follows a normal distribution then an optimal estimate for h is

#KERNEL DENSITY ESTIMATION PDF#

This results in a smaller standard deviation the estimate places more weight on the specific data value and less on the neighboring data values.īandwidths that are too small result in a pdf that is too spiky, while bandwidths that are too large result in a pdf that is over-smoothed.

You can use a smaller bandwidth value when the sample size is large and the data are densely packed.

This results in a larger standard deviation the estimate places more weight on the neighboring data values. Stute obtained in 1982 some valuable results on convergence rates of the estimator, depending on the sample size, kernel and true density.

You should use a larger bandwidth value when the sample size is small and the data are sparse.

Rules for choosing an optimum value for h are complex, but the following are some simple guidelines: I highly recommend it because you can play with bandwidth, select different kernel methods, and check out the resulting effects. The results are sensitive to the value chosen for h. There is a great interactive introduction to kernel density estimation here. Let be a random sample from some distribution whose pdf f( x) is not known. f(- x) = f( x).Ī kernel density estimation ( KDE) is a non-parametric method for estimating the pdf of a random variable based on a random sample using some kernel K and some smoothing parameter (aka bandwidth) h > 0. KDE #KDE data <- c(65, 75, 67, 79, 81, 91) plot(NA,NA,xlim = c(50,120),ylim = c(0,0.04),xlab = 'X',ylab = 'K (= density)') h = 5.5 kernelpoints <- seq(50,150,1) kde <- NULL for(i in 1:length(data)) lower = 1 upper = 10 tol = 0.01 #Using optimize function in R obj <- optimize(fmlcv ,c(lower,upper),tol=tol,maximum = TRUE) print(obj) plot(density(x), lwd = 4, col = 'purple') #From R library lines(density(x, bw = obj$maximum), lwd = 2, col = 'red', lty = 1) legend("topright",legend=c("KDE from R", "KDE from MLCV"), col=c("blue","red"),lty=1, cex=0.8, lwd = c(4,2),text.A kernel is a probability density function (pdf) f( x) which is symmetric around the y axis, i.e. The symmetric property of kernel function enables the maximum value of the function ( max(K(u)) to lie in the middle of the curve. This can be mathematically expressed as K (-u) = K (+u). This means the values of kernel function is same for both +u and –u as shown in the plot below.

The first property of a kernel function is that it must be symmetrical.

This function is also used in machine learning as kernel method to perform classification and clustering. Kernel functions are used to estimate density of random variables and as weighing function in non-parametric regression. Kernel density estimation is a technique for estimation of probability density function that is a must-have enabling the user to better analyse the studied probability distribution than when using. Kernel is simply a function which satisfies following three properties as mentioned below.

#KERNEL DENSITY ESTIMATION CODE#

All computations are coded in R from scratch and the code is provided in the last section of the article. Maximum likelihood cross-validation method is explained step by step for bandwidth optimization. One particularly useful metric is the Haversine distance which measures the angular distance between points on a sphere. Gaussian kernel is used for density estimation and bandwidth optimization. The kernel density estimator can be used with any of the valid distance metrics (see DistanceMetric for a list of available metrics), though the results are properly normalized only for the Euclidean metric. In comparison to parametric estimators where the. In this article, fundamentals of kernel function and its use to estimate kernel density is explained in detail with an example. Kernel density estimators belong to a class of estimators called non-parametric density estimators. In order to reduce bias, we intuitively subtract an estimated bias term from.

Kernel Construction and Bandwidth Optimization using Maximum Likelihood Cross Validation In this paper two kernel density estimators are introduced and investigated.